研究背景・目的
最短路クエリとは、与えられたネットワークに対して二点を指定し、その二点の間の距離は何かと聞くクエリのことです。最短路クエリはネットワークに対する基礎的なクエリであり、ウェブ検索における現在見ているウェブページを利用したランキング、ソーシャルネットワークにおける友人関係を利用したランキング、これらのネットワークの性質の解析など、様々な応用があります。本研究では特にこれらのネットワーク(総称して複雑ネットワークと呼ばれる)に対象を絞ります。本研究の目的は、前処理時間、インデックスサイズ、クエリ応答時間に関して、既存の手法よりも良いトレードオフを達成する手法を開発することです。
研究内容
本手法で作るインデックスは非常に単純な構造をしています。即ち、各頂点に対して、いくつかの他の頂点との間の距離を保存しておきます。これをその頂点のラベルと呼びます。二点u, vがクエリとして指定されたら、その二点のラベルの中で、共通の頂点wを探します。ラベルを利用してuとwの距離、vとwの距離が分かるので、その和を出力します。全頂点から幅優先探索をするのが一番単純なラベルの作り方ですが、これはインデックスが非常に大きくなり現実的ではありません。そこで本手法では簡単な枝刈りを導入しています。
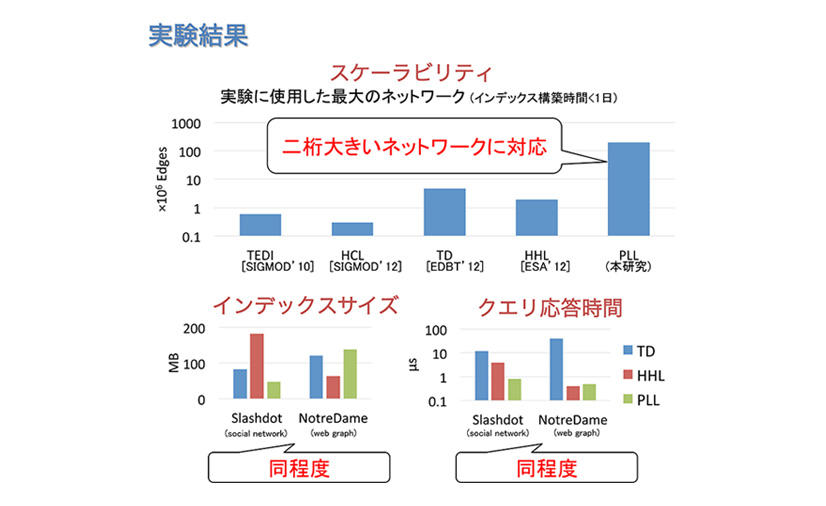
この枝刈りは、複雑ネットワークが「ハブ」を持つという性質を上手に利用しており、これによって既存の手法よりも二桁大きいネットワークが扱えるようになりました。勿論、枝刈り後も最短距離を正しく計算できます。本手法はその単純さから様々な亜種に対応できます。例えば枝に重みや向きが付いていても問題ありません。この様な亜種に対しても、既存の手法と同等かそれ以上の性能を出すことが出来ます。
産業応用の可能性
- ウェブグラフやソーシャルネットワークを利用した検索におけるランキング
- ウェブグラフやソーシャルネットワーク中の影響力の高い頂点の発見
- その他、通信ネットワークや代謝ネットワークへの応用
連絡先
吉田 悠一[情報学プリンシプル研究系 助教]
http://research.nii.ac.jp/~yyoshida/index.html


