研究背景・目的
コンピュータで計算を行うためのアルゴリズムの研究は大きな発展を遂げてきました。さまざまな問題に対して効率的に働くアルゴリズムが数多く開発されてきた一方で、その効率化に限界も見えてきました。例えば、広く信じられているP≠NP予想の下では、どんなNP困難問題も多項式時間で解くことはできません。また充足可能性問題(SAT)の難しさに関する「SETH」という仮定を用いると、グラフ理論における「到達可能性クエリ」を従来の方法より良くすることはできないのです。しかし、これらの効率化の限界は想定し得る全てのケースを考えた場合の限界であって、実際に扱いたい特殊なケースに限れば、必ずしもあてはまるわけではありません。また、対象が非常に大規模なグラフだったとしても、到達可能性クエリなど、効率的に処理できているものもあります。そのような実際の応用時に現れる特殊なケースに対して、効率的に働くアルゴリズムの開発とその解析を行っています。
研究内容
- 最短路クエリ問題
グラフ理論における「最短路クエリ」は、ネットワーク上の2点についての最短距離を聞く極めて重要な方法で、幅広く応用されています。しかし、これは一般的に考えると、従来の方法からの改善は見込めません。一方、「現実の大規模グラフ」は言うなれば「核」と「房」からなる「樹木のような」特殊な構造をしていることが知られています。そこで、私たちはその樹木のような構造を表す「木幅」という微細な指標に対しても効率的に入力できるアルゴリズムを設計し、現実のグラフに対して非常に効率的に動作することを実験で証明しました。 - 分枝限定法
「 分枝限定法」は、易しくして解きやすくした緩和問題の解を用いて探索(枝刈り探索)を行う、「NP困難問題」を解くために広く用いられている汎用手法です。しかし理論上で想定し得る最悪のケースが起こった場合、枝刈り探索をしないで全探索を行うのと同じような手間がかかってしまい、極めて効率が悪くなります。そこで、実際には緩和問題と元の問題の解が比較的近いことに着目し、それがあてはまるケースについては、枝刈りなしの全探索よりも遥かに効率的に動作することを理論的に証明しました。
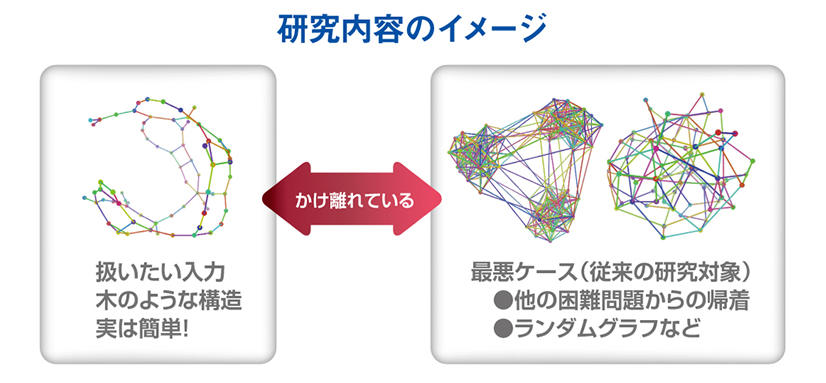
「一般には難しい」=「とても難しい入力が存在」全部が難しいわけではない
産業応用の可能性
- 大規模ウェブ・ソーシャルグラフに対する距離や関連度などのクエリ処理、クラスタリングなどのデータマイニングに対する効率的なアルゴリズム開発
- モデル検査、静的解析、プランニングなど、個々の目的に特化したより効率的なソルバ開発
研究者の発明
- 特開2015-184704:ネットワーク管理装置、ネットワーク管理方法及びプログラム
連絡先
岩田 陽一[情報学プリンシプル研究系 助教]
yiwata[at]nii.ac.jp ※[at]を@に変換してください
Recommend
さらにみる


