量子情報キーワード解説
Feshbach Resonance
2つの粒子の間の低エネルギー散乱を考える。対象としている粒子にいくつかのエネルギー準位があり、それに付随した束縛状態が2粒子間に形成されている場合で、特に、その束縛エネルギーが、2粒子間の散乱時のエネルギーと近いときに、散乱状態(open channel)と束縛状態(closed channel)との相互作用により、共鳴的に散乱状態が変化する現象を指して、フェッシュバッハ共鳴(Feshbach Resonance)と言う。散乱状態と束縛状態の相対的なエネルギー差を磁場で制御する場合を、magnetic Feshbach Resonanceと言い、2粒子の束縛状態と散乱状態を光で結合させる場合を、optical Feshbach Resonance と言っている。
BEC-BCS cross over
フェッシュバッハ共鳴(Feshbach Resonance)等の手法により、二つのフェルミ粒子間の結合を大きく変化させたときに、2粒子間の結合が弱く運動量空間でペアー(クーパーペア)を形成しているとみなせるBCS(バーディーン・クーパー・シュリーファー)領域から、2粒子間の結合が強く実空間でペアー(分子)を形成しているとみなせる(分子の)BEC(ボース・アインシュタイン凝縮)領域に、連続的に変化する現象。この変化は量子相転移ではないため、クロスオーバーという。
Recoil energy
質量Mの単一の原子を考え、それと波数kの光が相互作用する状況を考える。このとき、(hk/(2π))2/(2M)は、原子が運動量として単一光子の運動量hk/(2π)を持ったときの、原子の運動エネルギーに対応しており、これを特に、(単一光子)Recoil energy(反跳エネルギー)と呼んでいる。ここで、hはプランク定数である。特に、光格子などのトラップ中に閉じ込められた原子系における基本的なエネルギー尺度を与えると同時に、自由空間では、共鳴のシフトとして現れる。また、光の吸収を使ったレーザー冷却法において、その到達限界温度はこの反跳エネルギーのオーダーになる。
T1, T2, T2*
量子情報処理において量子ビットとして用いられる2準位系に対して、そのデコヒーレンスを表すパラメーターとして導入される時定数。T1はエネルギー緩和時間または縦緩和時間とも呼ばれ、2準位系を密度行列で表したときの対角項である占拠数(population)に対する(または、パウリ演算子Zの)緩和の時定数を与え、T2は位相緩和時間または横緩和時間とも呼ばれ、2準位系を密度行列の非対角項であるコヒーレンス(coherence)に対する(または、パウリ演算子XおよびYの)緩和の時定数を与る。また、2準位系の集合を対象としたときに、何がしかの不均一性によりそのエネルギーに広がりが生じている場合には、それが原因で集団全体でのコヒーレンスが緩和する。この緩和の時定数を、均一な集団の時の緩和時間T2と区別して、T2*と表記する。
Hong-Ou-Mandel干渉
透過率、反射率がともに50%の半透鏡の両面から、同じ入射角で光子を1個ずつ入射した時に見られる二光子干渉効果。もし、二光子が区別可能な古典粒子であれば、(a)両光子とも透過、(b)両光子とも反射、(c)光子1は透過し光子2は反射、(d)光子1は反射し光子2は透過、の4つの事象はそれぞれ25%の確率で起こると考えられる。実際には光子はボソンなので、(c)や(d)の場合に半透鏡の同じ側に出た二光子が原理的に区別できないように調整されていると、干渉が生じ、(a)と(b)の確率がゼロになる。逆に、この確率がゼロでなければ、その大きさが二光子の空間・時間モード形状の不一致の度合いを与えることになる。とくに、二光子の入射の時間差を変えながらこの確率を測定してグラフを書くと、光子の波束の幅を反映した幅をもつディップが得られるので、二光子のタイミングの調整によく用いられる。
この干渉の解釈はいろいろあるが、(c)や(d)のように二光子が同じモードに入ろうとすると、ボゾンの増強効果で確率が二倍になり、その分(a)と(b)が減ってゼロになると考えればよい。あるいは、半透鏡における状態変化の法則から、(a)と(b)の終状態を計算すると、位相が反対の同じ状態になり、和をとるとキャンセルして消えるのが確かめられる。
Fidelity(忠実度)
2つの量子状態がどのくらい近いかを示す指標のひとつ。同一ならば1、互いに直交するなら0になる。2状態がどちらも純粋状態ならば、状態ベクトルの内積の大きさの2乗がFidelityを与える。とくに実験結果の解析に用いられる場合は、理想的な状態(純粋状態)と、実際に生成された量子状態(混合状態)のFidelityを考えることが多い。この場合、混合状態の密度演算子を純粋状態のケット、ブラで挟んだものがFidelityを与える。この値は、実際に生成された量子状態が、「理想的な状態か否か」という直交測定による試験に合格する確率、という明確な意味を持つ。
2状態ともに混合状態の場合は、上記の例を含むように自然に拡張するやり方として、仮想的な補助系を考え、各混合状態のpurification(全系の純粋状態で、補助系を捨てればもとの混合状態に一致するもの)の間の内積の大きさの2乗の最大値をFidelityとする。この一般の定義では、その値自体に明確な意味付けを与えるのは困難であるが、どのような物理操作によっても決して減少しない量であることは簡単に証明できるので、量子状態の「近さ」を表す原理的な指標としての最低限の要件は満たされている。
尚、上記の定義の平方根をFidelityとする流儀もあるので注意が必要である。
Allan variance(アラン分散)
原子時計、水晶振動子、等の発振器の安定度の指標。周波数![]() の発振器が時間的な揺らぎをもち、時刻
の発振器が時間的な揺らぎをもち、時刻![]() での瞬時周波数が
での瞬時周波数が![]() と表されるとき、
と表されるとき、![]() を規格化された周波数偏差という。周波数を
を規格化された周波数偏差という。周波数を![]() ゲート時間
ゲート時間![]() のカウンターで計測し、規格化された周波数偏差の
のカウンターで計測し、規格化された周波数偏差の![]() 番目の平均値を、
番目の平均値を、![]() とするとき、アラン分散は
とするとき、アラン分散は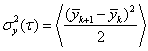 によって定義される。通常の分散は全サンプルの平均値からのずれの2乗和を計算するのに対し、アラン分散では連続する測定値の差の2乗和を計算することから、位相揺らぎが低域で大きな成分をもつときにも発散しない。
によって定義される。通常の分散は全サンプルの平均値からのずれの2乗和を計算するのに対し、アラン分散では連続する測定値の差の2乗和を計算することから、位相揺らぎが低域で大きな成分をもつときにも発散しない。
原子時計は、2準位原子にラジオ波またはレーザーなどを照射したときの原子の状態変化を射影測定し、それら発振器の原子の共鳴周波数からのずれを読み出し、共鳴周波数に合うように発振器にサーボをかける。このとき、![]() の揺らぎを決めるのは
の揺らぎを決めるのは![]() 個の原子の射影測定に伴う量子揺らぎ
個の原子の射影測定に伴う量子揺らぎ![]() となる。この結果、原子時計のアラン偏差(Allan deviation)は
となる。この結果、原子時計のアラン偏差(Allan deviation)は![]() と表される。ただし
と表される。ただし![]() は観測する原子遷移の
は観測する原子遷移の![]() 値、
値、![]() は
は![]() 時間に観測される原子数である。
時間に観測される原子数である。
Optical frequency comb (光周波数コム)
フェムト秒レーザーとも呼ばれる超短パルスレーザーを周波数軸上で眺めると、パルスの繰返し周波数![]() 間隔で並んだ広帯域な櫛(コム、comb)状の光スペクトルとなっていることに由来する。周波数の原点付近から測って、この
間隔で並んだ広帯域な櫛(コム、comb)状の光スペクトルとなっていることに由来する。周波数の原点付近から測って、この![]() 番目の櫛に対応する光の周波数は、繰返し周波数
番目の櫛に対応する光の周波数は、繰返し周波数![]() とオフセット周波数を
とオフセット周波数を![]() 使って、
使って、![]() と表される。この周波数の近傍に測りたい周波数
と表される。この周波数の近傍に測りたい周波数![]() があるとき、RF周波数のビート
があるとき、RF周波数のビート![]() および、RF周波数の
および、RF周波数の![]() 、
、![]() をカウンターで測定すると、
をカウンターで測定すると、![]() として光周波数が決定できる。ここで、
として光周波数が決定できる。ここで、![]() は
は![]() が100 MHz程度以上あれば波長計で容易に計測可能で、また
が100 MHz程度以上あれば波長計で容易に計測可能で、また![]() をわずかに調整するときの
をわずかに調整するときの![]() の変化から、その符号が決定できる。
の変化から、その符号が決定できる。
Stoner模型
金属強磁性が、格子模型において電子間斥力相互作用のためにどのように現れるかを、単一バンドのハバード模型に対して平均場近似(Hartree-Fock近似)で扱った理論。金属強磁性(フェルミオンが格子点の間を跳び移れる模型における強磁性で、バンド強磁性とも呼ばれる)に対する最も簡単な理論。この理論では、2個のフェルミオンが同じ格子点に来た場合の斥力相互作用 (![]() ) が、フェルミ面の状態密度(
) が、フェルミ面の状態密度(![]() ) の逆数程度より大きくなれば基底状態は常磁性から強磁性になるであろうという結論される。相転移を評価するには、バンド強磁性状態(磁化(
) の逆数程度より大きくなれば基底状態は常磁性から強磁性になるであろうという結論される。相転移を評価するには、バンド強磁性状態(磁化(![]() 電子数-
電子数-![]() 電子数)をもつ状態)と、常磁性状態のエネルギーをHartree-Fock近似の範囲で比較すると、斥力は上下スピンの個数がアンバランスになった方が効きにくいので、
電子数)をもつ状態)と、常磁性状態のエネルギーをHartree-Fock近似の範囲で比較すると、斥力は上下スピンの個数がアンバランスになった方が効きにくいので、![]() の得(減少)をする(
の得(減少)をする(![]() は全格子点の数)。一方、スピンを揃えると運動エネルギーは
は全格子点の数)。一方、スピンを揃えると運動エネルギーは![]() だけ損(増加)してしまう。結局、全エネルギー変化は、これらのトレードオフとなり、合計
だけ損(増加)してしまう。結局、全エネルギー変化は、これらのトレードオフとなり、合計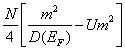 が強磁性状態の方が低くなる条件(ストーナー条件)は、
が強磁性状態の方が低くなる条件(ストーナー条件)は、![]() である。この議論は強磁性を考察する上で教科書的とされてきたが、強磁性状態の安定性を過大評価している。実際、近似を上げて電子相関による補正を入れていくと、強磁性転移点
である。この議論は強磁性を考察する上で教科書的とされてきたが、強磁性状態の安定性を過大評価している。実際、近似を上げて電子相関による補正を入れていくと、強磁性転移点![]() は大きくなっていく。
は大きくなっていく。
長岡強磁性
一番単純な電子相関の模型であるハバード模型において、電子相関を厳密に取り入れて強磁性が起き得る場合があることを示した、歴史的に最初であり、現在でも数少ない例。ストーナー条件は不十分であり、電子相関を取り入れていくにつれて条件は厳しくなるが、それでも強磁性が厳密に残る場合はあるか、という疑問に答える。正方格子や立方格子ではハーフ・フィリング(フェルミオン数が格子点数に等しい場合)においては反強磁性絶縁体となる。ここでフェルミオン数をずらせて正孔を導入すると、この正孔は動き回る。よって、この運動エネルギーと磁性相互作用との競争になる。長岡が示したのは、「ハーフ・フィリングに唯一個正孔をドープ(したがって、全格子点数![]() が十分大きい場合はドーピング量としては無限小)しただけでも、この正孔の運動のせいで、
が十分大きい場合はドーピング量としては無限小)しただけでも、この正孔の運動のせいで、![]() の極限では基底状態は強磁性となる」。電子相関を起源にもつだけあって、この長岡状態は普通のストーナー 強磁性とは異なる。つまり、
の極限では基底状態は強磁性となる」。電子相関を起源にもつだけあって、この長岡状態は普通のストーナー 強磁性とは異なる。つまり、![]() を無限に大きくしてストーナー条件を極端に満たさせたのだから、平均場的描像は成り立っていそうだと一見思われるが、実は全く異なる強相関極限である。但し、長岡強磁性は、
を無限に大きくしてストーナー条件を極端に満たさせたのだから、平均場的描像は成り立っていそうだと一見思われるが、実は全く異なる強相関極限である。但し、長岡強磁性は、![]() の極限であり、かつドーピング量が無限小、という二重の極限操作が必要な強磁性であり、実際、有限温度にすると壊れる、といった不安定な強磁性である。
の極限であり、かつドーピング量が無限小、という二重の極限操作が必要な強磁性であり、実際、有限温度にすると壊れる、といった不安定な強磁性である。
平坦バンド強磁性
長岡強磁性とは異なり、![]() が任意(0から
が任意(0から![]() )の場合に存在し、しかも安定な強磁性基底状態として厳密にもつ模型が平坦バンド強磁性である。機構としては、強磁性が基底状態であることを、多体状態に対するフロベニウスの定理を使って証明する、という点で長岡強磁性と共通する。考える系は、一体の(フェルミオン間の相互作用を切った)バンド構造が分散のない平坦なバンドを含むような格子を考える。直感的には、バンドが平坦であれば、磁化をもたせた場合の運動エネルギーの損がないため強磁性になり易いと思えるが、実はそのような平均場効果ではなく電子相関効果のために強磁性となる。実際、平坦ならどんなバンドでも良い訳ではなく、数学的にはさらに、connectivityと呼ばれる条件が必要である。これにより、平坦バンドがハーフフィルドの場合に、基底状態が強磁性(正確にはフェリ磁性の場合もある)であることが厳密に証明される。この磁性は、安定であり、有限温度にしたり、平坦バンドに少し分散をもたせたりしても安定である。分子に対する量子化学においては、non-bonding molecular orbital (NBMO)と呼ばれる軌道上ではフントの規則により高スピン状態になるが、平坦バンドをもつ結晶においては格子点数だけNMBOか生じ、そのバンド上でのフント結合(交換相互作用)の効果と見なすこともできる。
)の場合に存在し、しかも安定な強磁性基底状態として厳密にもつ模型が平坦バンド強磁性である。機構としては、強磁性が基底状態であることを、多体状態に対するフロベニウスの定理を使って証明する、という点で長岡強磁性と共通する。考える系は、一体の(フェルミオン間の相互作用を切った)バンド構造が分散のない平坦なバンドを含むような格子を考える。直感的には、バンドが平坦であれば、磁化をもたせた場合の運動エネルギーの損がないため強磁性になり易いと思えるが、実はそのような平均場効果ではなく電子相関効果のために強磁性となる。実際、平坦ならどんなバンドでも良い訳ではなく、数学的にはさらに、connectivityと呼ばれる条件が必要である。これにより、平坦バンドがハーフフィルドの場合に、基底状態が強磁性(正確にはフェリ磁性の場合もある)であることが厳密に証明される。この磁性は、安定であり、有限温度にしたり、平坦バンドに少し分散をもたせたりしても安定である。分子に対する量子化学においては、non-bonding molecular orbital (NBMO)と呼ばれる軌道上ではフントの規則により高スピン状態になるが、平坦バンドをもつ結晶においては格子点数だけNMBOか生じ、そのバンド上でのフント結合(交換相互作用)の効果と見なすこともできる。
以上、Stoner模型、長岡強磁性、平坦バンド強磁性に関して詳しくは、草部浩一、青木秀夫:「強磁性」(青木秀夫監修:多体電子論、第I巻;東京大学出版会、1998)を参照。
Purcell Factor
原子が微小な高Q共振器中にあるとき、共振器で定義される特定の電磁場モードへの遷移確率の増強が観測される(Purcell効果)。原子からの輻射増強の自由空間にある場合との比を Purcell Factor と呼ぶ。共鳴条件において原子が共振器電場の極大に位置する場合には次式で与えられる。
![]()
ここで、![]() は材質中の電磁場の波長、
は材質中の電磁場の波長、![]() ,
, ![]() は、それぞれ共振器の
は、それぞれ共振器の![]() 値 ,波長を単位に測ったモード体積。
値 ,波長を単位に測ったモード体積。
真空ラビ分裂
原子などの量子2準位系では、それと共鳴するコヒーレントな光との相互作用により、2準位系があたかも光の衣を纏ってエネルギー的に分裂した新しい状態(dressed state)が形成される。そのとき観測される状態間のエネルギー分裂はラビ(Rabi)分裂と呼ばれるが、特に2準位系と相互作用する光子数が1個のときは2準位系が上準位にあるときに電磁場が真空であることから真空ラビ分裂と呼ばれる。通常、光子1個と原子1個の相互作用は極めて微弱なため、真空ラビ分裂は自然幅などに隠れて観測されないが、共振器を用いて電磁場を増強したり、巨大な双極子モーメントをもつ Rydberg 状態と呼ばれるイオン化寸前の原子を使い相互作用を増強するとはじめて観測可能となる。この研究分野は共振器量子電磁気学(cavity QED:Quantum Electro Dynamics)と呼ばれる。光子が量子2準位系と共振器の間で交換される時間が、共振器中の光子寿命や量子2準位系の寿命に比べて短い いわゆる「強結合条件」を実現することで、物質と光の量子力学的なダイナミクスを光子1個レベルで解明することが可能となる。近年、自然の原子以外でも、例えば、微細加工技術で作製された半導体量子ドットや、超伝導ジョセフソン回路の人工原子状態とマイクロ波の組み合わせによる cavity/回路 QED の実験報告が顕著に増えている。
SO(3)
SO(3)は、3次元空間における回転操作群を表す群論での表記である。例えば、ある方向を向いた3次元ベクトルがあるとする。そのベクトルは回転によって、長さが等しく方向が異なるベクトルに変換できる。この回転に相当する演算子を![]() と書く。ここで、
と書く。ここで、![]() はベクトルの回転角、
はベクトルの回転角、![]() は回転軸の方向を指した単位ベクトルである(図1参照)。一般的には、2つの回転を合成したものも回転になる。この特性から
は回転軸の方向を指した単位ベクトルである(図1参照)。一般的には、2つの回転を合成したものも回転になる。この特性から![]() は群を形成することがわかる。
は群を形成することがわかる。
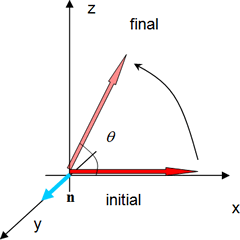
図1:3次元のベクトルの回転
回転の具体的な例として、x,y,z軸まわりの回転をそれぞれ以下のように書くことができる。
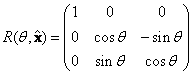
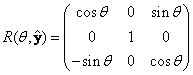
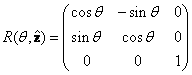
これらの回転を合成することによって、任意の回転を作ることができる。
![]()
量子情報でよく用いられる関係の一つとして、SU(2)の群はSO(3)と同型(isomorphic)であることが知られている。SU(2)は行列式が1の2x2ユニタリ行列が為す群である。SU(2)の例としては、qubitスピンの回転が最もよく知られている。スピン1/2の場合、一般的なSU(2)の回転は
![]()
と表せる。ここで、SU(2)とSO(3)の同型性から、2次元ベクトルであるqubitの状態
![]()
を、ブロッホ球(Bloch sphere)上に終点を持つ3次元ベクトルとして可視化することができる(図2参照)。この時、ブロッホ球中の角度θ, φと|ψ>の展開係数a, bの関係は
![]()
となる。この関係によって、qubitの状態変換なども直感的に可視化することができる。
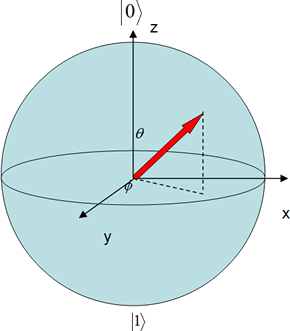
図2:ブロッホ球

